Kirchhoff’s Laws

Two extremely important principles in electric circuits were codified by Gustav Robert Kirchhoff in the year 1847, known as Kirchhoff’s Laws. His two laws refer to voltages and currents in electric circuits, respectively.

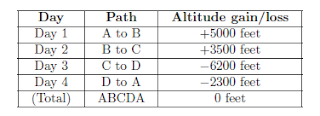
Kirchhoff’s Voltage Law states that the algebraic sum of all voltages in a closed loop is equal to zero. Another way to state this law is to say that for every rise in potential there must be an equal fall, if we begin at any point in a circuit and travel in a loop back to that same starting point. An analogy for visualizing Kirchhoff’s Voltage Law is hiking up a mountain. Suppose we start at the base of a mountain and hike to an altitude of 5000 feet to set up camp for an overnight stay. Then, the next day we set off from camp and hike farther up another 3500 feet. Deciding we’ve climbed high enough for two days, we set up camp again and stay the night. The next day we hike down 6200 feet to a third location and camp once gain. On the fourth day we hike back to our original starting point at the base of the mountain. We can summarize our hiking adventure as a series of rises and falls like this:

Of course, no one would tell their friends they spent four days hiking a total altitude of 0 feet, so people generally speak in terms of the highest point reached: in this case 8500 feet. However, if we track each day’s gain or loss in algebraic terms (maintaining the mathematical sign, either positive or negative), we see that the end sum is zero (and indeed must always be zero) if we finish at our starting point.

If we view this scenario from the perspective of potential energy as we lift a constant mass from point to point, we would conclude that we were doing work on that mass (i.e. investing energy in it by lifting it higher) on days 1 and 2, but letting the mass do work on us (i.e. releasing energy by lowering it) on days 3 and 4. After the four-day hike, the net potential energy imparted to the mass is zero, because it ends up at the exact same altitude it started at.

Let’s apply this principle to a real circuit, where total current and all voltage drops have already been calculated for us:

If we trace a path ABCDEA, we see that the algebraic voltage sum in this loop is zero:

We can even trace a path that does not follow the circuit conductors or include all components,

such as EDCBE, and we will see that the algebraic sum of all voltages is still zero:

Kirchhoff’s Voltage Law is often a difficult subject for students, precisely because voltage itself is a difficult concept to grasp. Remember that there is no such thing as voltage at a single point; rather, voltage exists only as a differential quantity. To intelligently speak of voltage, we must refer to either a loss or gain of potential between two points.